1. 피드 포워드 신경망(Feed-Forward Neural Network, FFNN)
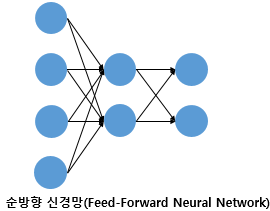
오직 입력층에서 출력층 방향으로 연산이 전개되는 신경망
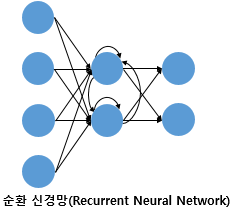
FFNN가 아닌 RNN이라는 신경망이다. 은닉층의 출력값을 출력층으로도 값을 보내지만, 동시에 은닉층의 출력값이 다시 은닉층의 입력으로 사용되기도 한다.
2. 전결합층(Fulyy-connected layer, FC, Dence layer)
다층 퍼셉트론은 은닉층과 출력층에 있는 모든 뉴런은 바로 이전 층의 모든 뉴런과 연결되어 있다.전결합층 (완전결합층, FC): 이전 층의 모든 뉴런과 연결되어 있는 층밀집층이라고 부르기도 한다.
3. 활성화 함수(Activation Function)
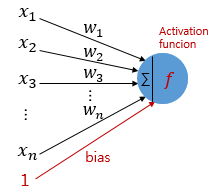
은닉층과 출력층의 누련에서 출력값을 결정하는 함수
계단 함수(0 or 1)는 활성화 함수의 하나의 예제에 불과하다.
(1) 활성화 함수의 특징 - 비선형 함수(Nonlinear function)
활성화 함수는 선형 함수가 아니라 비선형 함수다. 즉 f(x) = wx + b라는 꼴로 표현할 수 없는, 직선 1개로는 그릴 수 없는 함수다.
🤔 why?: f(x) = wx라고 가정하면 은닉층을 두개 통과해봐야 y(x) = f(f(f(x)))가 되는데 식으로 xw^3가 됨. 그러면, 곧 w의 세 제곱 값을 k라고 정의하면 y(x) = kx와 같이 표현이 다시 된다. 그렇다는건 선형 함수로 은닉층을 여러번 추가하더라도 1회 추가한 것과 차이가 없다.
그러나 종종 활성화 함수를 사용하지 않는 층을 비선형 층들과 함께 선형 함수 층을 인공 신경망의 일부로서 추가하는 경우가 있다. ➡️ 학습 가능한 가중치가 새로생긴다는 점에서 의미가 있다.
선형 함수를 사용한 층: 선형층(linear layer),투사층(projection layer)등의 표현을 사용하여 표현
ex. 임베딩 층도 일종의 선형층! ➡️ 활성화 함수가 존재하지 않음.
(2) 계단 함수(Step function)
퍼셉트론을 통해 인공 신경망을 처음 배울 때 접하게 되는 활성화 함수이다.(거의 사용 안됨)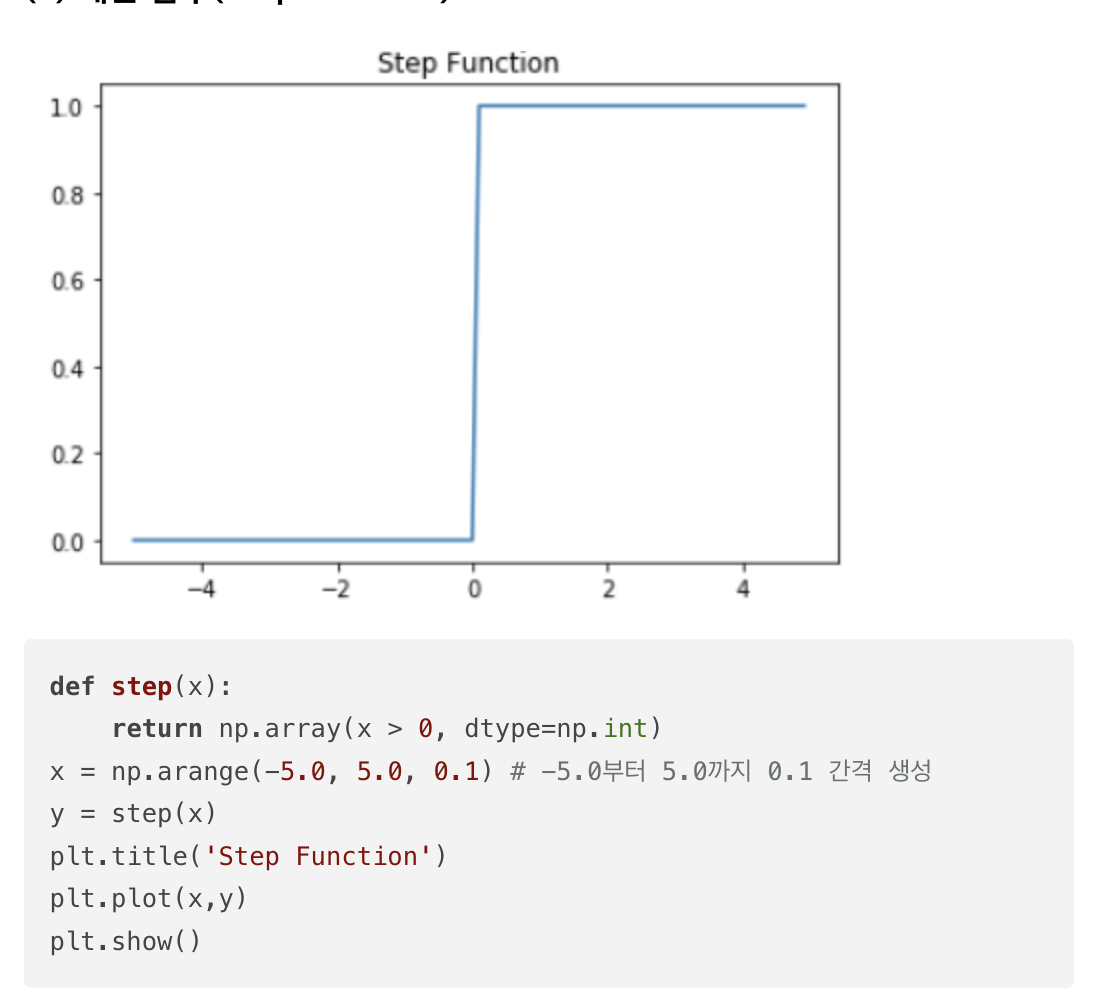
(3) 시그모이드(Sigmoid function)와 기울기 소실
시그모이드 함수를 사용한 인공 신경망이 있다고 가정하자.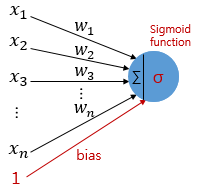
- 인공 신경망은 입력에 대해서 순전파 연산을 하고
- 순전파 연산을 통해 나온 예측값과 실제값의 오차를 손실함수로 계산하며
- 이 손실을 미분하여 기울기를 구하고
- 이를 통해 출력층에서 입력층 방향으로 가중치와 편향을 업데이트 하는 과정을 수행:
역전파
인공신경망은 역전파과정에서경사 하강법를 수행한다.
이 시그모이드 함수의 문제점은 미분을해서 기울기를 구할 때 발생한다.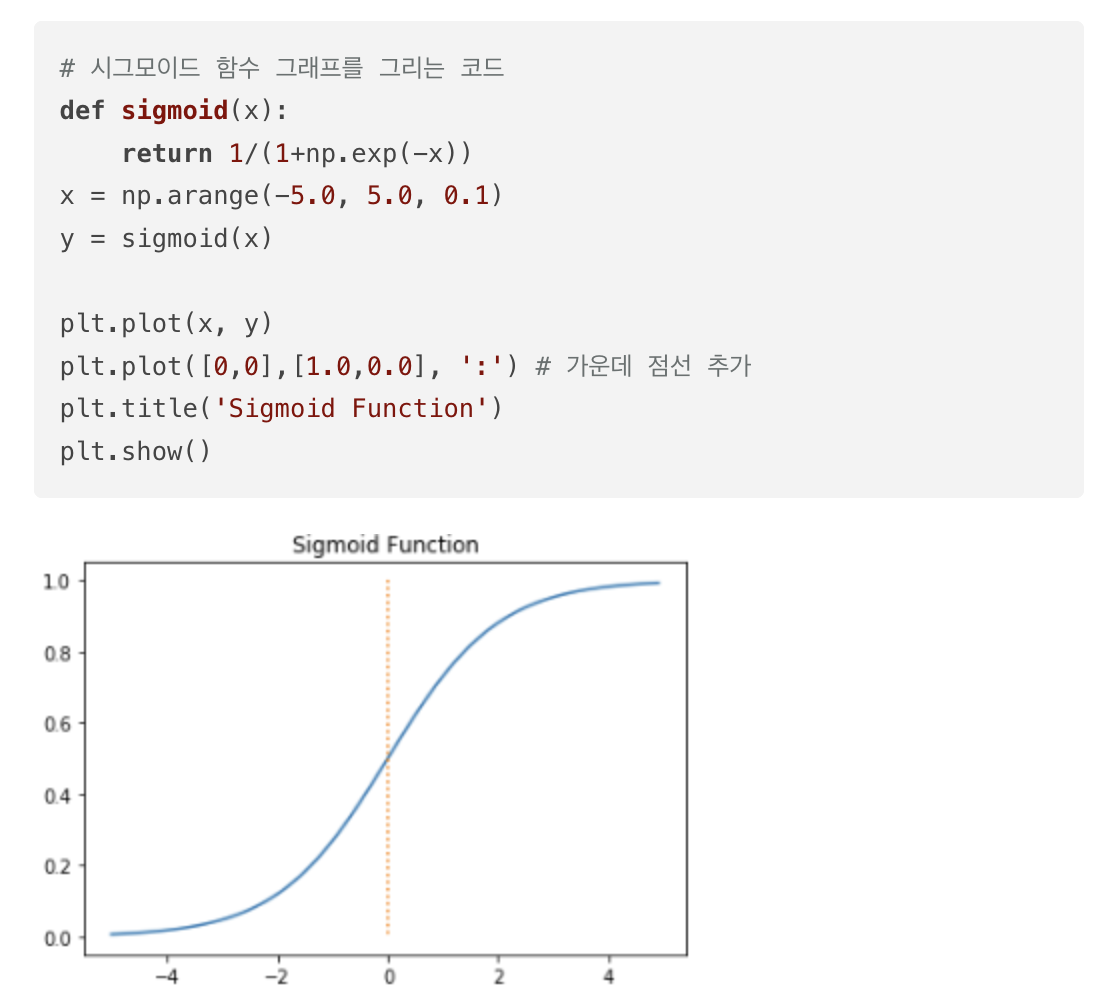
함수의 출력값이 0또는 1에 가까워질수록 그래프의 기울기가 완만해짐
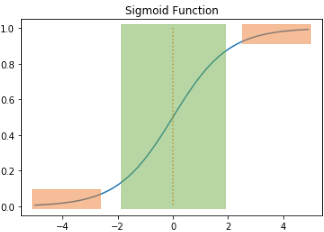
- 주황색 구간에서는 미분값이 0에 가까워짐
- 초록색 구간에서의 미분 값은 최대값이 0.25
역전파 과정(가중치와 편향을 업데이트하는 과정)에서 0에 가까운 값이 누적되면서 곱해지면, 앞단에는 기울기(미분값)가 잘 전달되지 않는다 ➡️ 기울기 소실
시그모이드 함수는 은닉층의 개수가 다수가 될 경우에는 0에 가까운 기울기가 계속 곱해지면 앞단에서는 거의 기울기를 전파받을 수 없다. (매개변수가 업데이트 되지 않아 학습이 되지 않는다.)
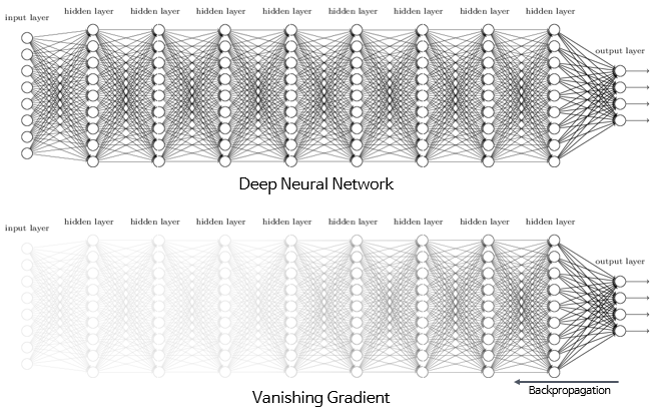
은닉층이 깊은 신경망에서 기울기 소실 문제로 인해 출력층과 가까운 은닉층에서는 기울기가 잘 전파되지만, 앞단으로 갈수록 기울기가 제대로 전파되지 않는 모습
- 시그모이드 함수는 은닉층에서 사용을 지양하자. (주로 이진분류를 위해 출력층에서 사용)
(4) 하이퍼볼릭탄젠트 함수(Hyper bolic tangent function)
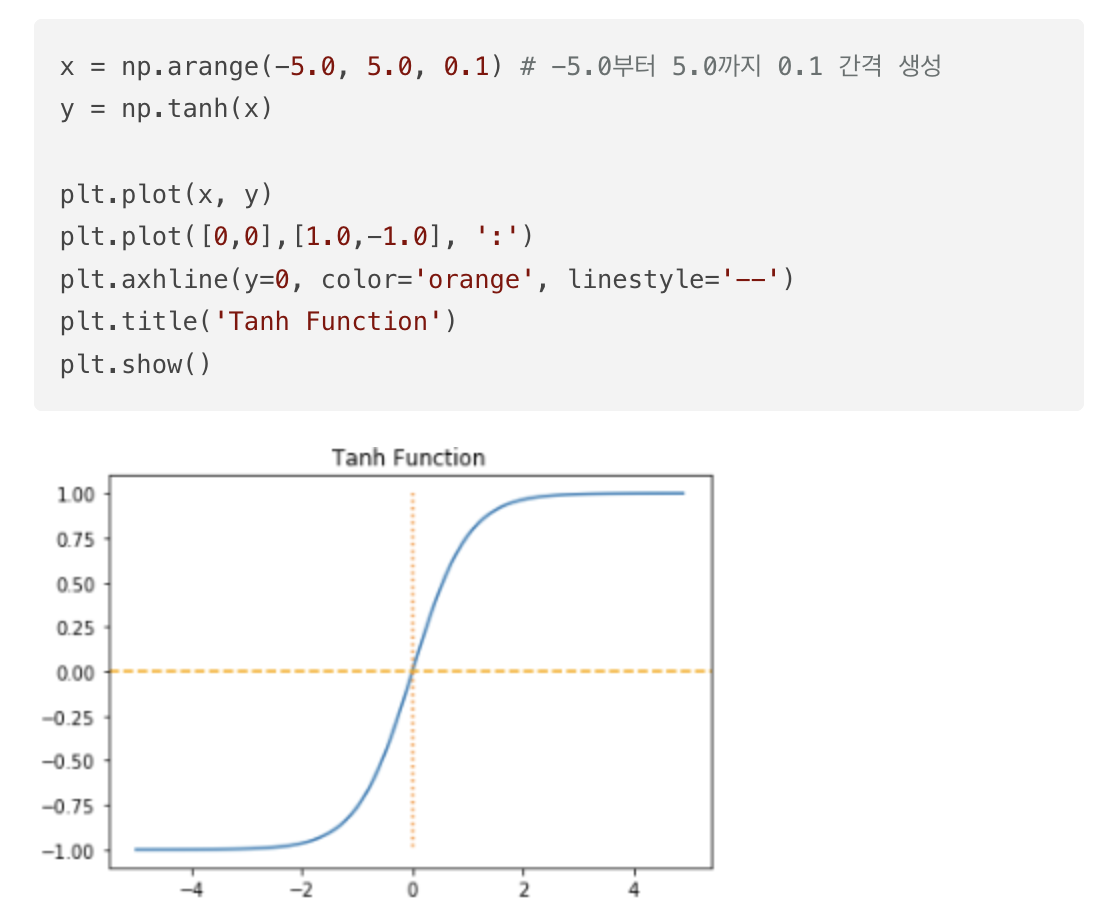
-1과 1에 가까운 출력값을 출력할 때, 시그모이드 함수와 같은 문제가 발생한다. 그러나 시그모이드보다는 전반적으로 큰 값이 나와서 기울기 소실 증상이 적은 편이기에 은닉층에서 시그모이드 함수보다는 선호된다.
(5) 렐루 함수(ReLU)
은닉층에서 가장 인기 있는 함수로, 수식은 f(x) = max(0,x)다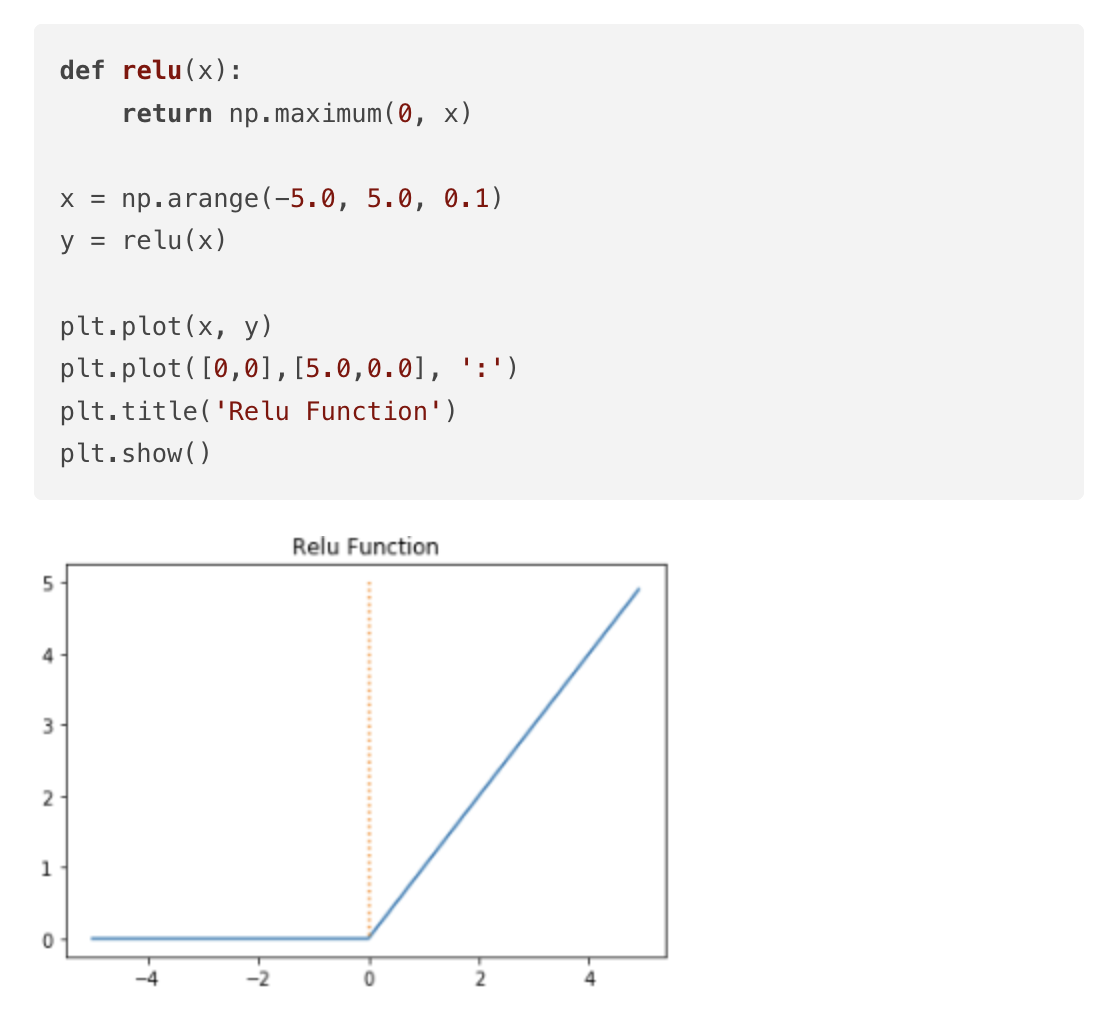
음수를 입력하면 0을 출력하고, 양수를 입력하면 입력값을 그대로 반환하는 함수이다.
0 이상의 입력값일 경우에는 미분값이 항상 1이다. ➡️ 깊은 신경망의 은닉층에서 시그모이드 함수보다 훨씬 더 잘 작동한다.
단순 임계값이므로 연산 속도도 빠르다.
그러나, 입력값이 음수면 미분값도 0이 되며, 이 뉴런은 회생하는게 매우 어려운 단점(죽은 렐루)이 있다.
(6) 리키 렐루(Leaky ReLU)
죽은 렐루를 보안하기 위한 ReLU등장의 변형 함수이다.
Leaky ReLU는 입력값이 음수일 때 0이 아니라 0.001과 같이 매우 작은 수로 반환하도록 되어있다. 수식은 f(x) = max(ax,x)로 매우 간단하다. a는 하이퍼파라미터로 새는 정도를 결정하며 일반적으로 0.01의 값을 가진다.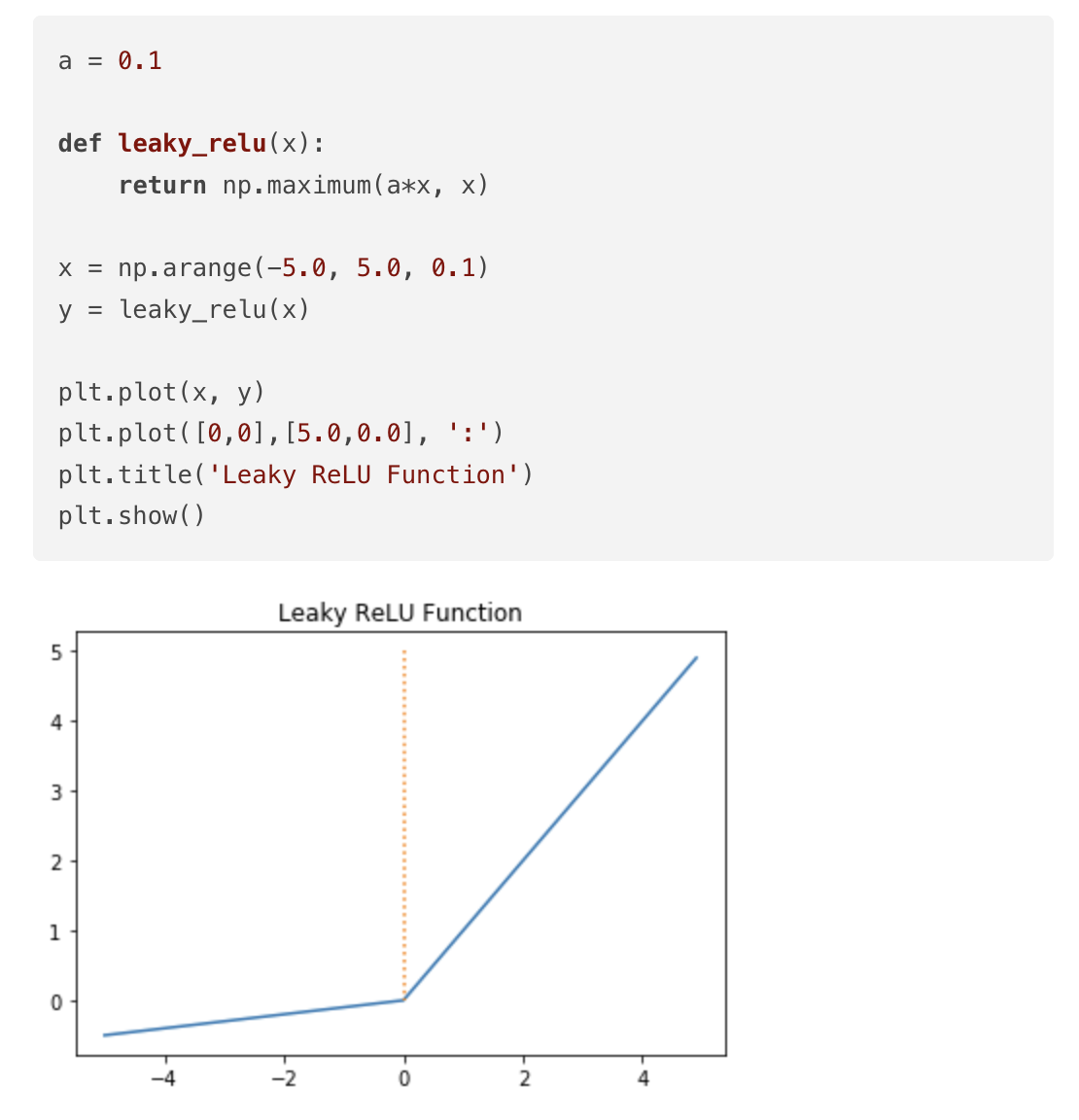
입력값이 음수라도 기울기가 0이 되지 않으면 ReLU는 죽지 않는다.
(7) 소프트맥스 함수(Softmax function)
은닉층에서는 ReLU함수들을 사용하는 것이 일반적이다. 소프트맥스 함수는 출력층에서 주로 사용된다.
- 시그모이드 함수 ➡️ 두 가지 선택지 중 하나를 고르는
이진 분류 문제➡️ 로지스틱 회귀 - 소프트맥스 함수 ➡️ 세 가지 이상의 (상호 배타적인) 선택지 중 하나를 고르는
다중 클래스 분류 문제➡️ 소프트맥스 회귀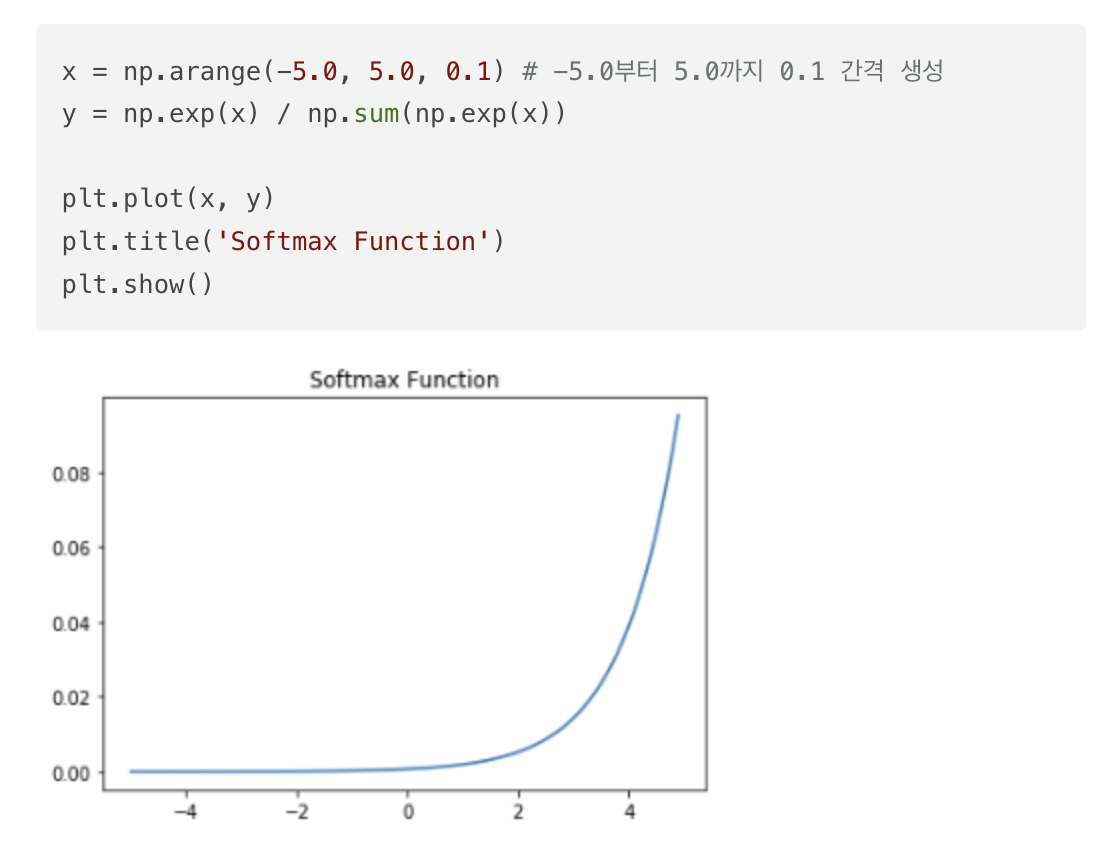
'ML' 카테고리의 다른 글
| 딥 러닝의 학습 방법 (1) | 2024.06.05 |
|---|---|
| 행렬곱으로 이해하는 신경망 (0) | 2024.06.05 |
| [핸즈온 머신러닝] 머신 러닝(Machine Learning) (0) | 2024.06.05 |
| [핸즈온 머신러닝] 선형 회귀(Linear Regression) (0) | 2024.06.05 |
| [핸즈온 머신러닝] 로지스틱 회귀(Logistic Regression) (0) | 2024.06.05 |