학습 데이터에 모델이 과적합되는 현상은 모델의 성능을 떨어뜨리는 주요 이슈이다. 훈련 데이터에 대한 정확도는 높을 지라도 검증 데이터나 테스트 데이터에 대해서는 제대로 동작하지 않는다. 불필요할 정도로 과하게 암기하여 훈련 데이터에 포함된 노이즈까지 학습된 상태이다.
1. 데이터의 양을 늘리기
모델은 데이터의 양이 적을 경우, 해당 데이터의 특정 패턴이나 노이즈까지 쉽게 암기하기 되므로 과적합 현상이 발생할 확률이 늘어난다. ➡️ 데이터의 양을 늘려서 데이터의 일반적인 패턴을 학습하여 과적합을 방지하자
만약, 데이터의 양이 적을 경우에는 의도적으로 기존의 데이터를 조금씩 변형하고 추가하여 데이터의 양을 늘리기도 하는데 이를 데이터 증식 또는 증강이라고 한다. 이미지의 경우에는 데이터 증식이 많이 사용되는디 이미지를 돌리거나 노이즈를 추가하고, 일부분을 수정하는 등으로 데이터를 증식시킨다.
텍스트 데이터의 경우에는 데이터를 증강하는 방법으로 변역 후 재번역을 통해 새로운 데이터를 만들어내는 역변역 등의 방법이 있다.
2. 모델의 봅작도 줄이기
인공 신경망의 복잡도는 은닉층의 수나 매개변수의 수 등으로 결정된다. 과적합 현상이 포착된다면, 인공신경망의 복잡도를 줄이는 것이다.
- 인공 신경망에서는 모델에 있는 매개변수들의 수를 모델의 수용력(capacity)이라고 하기도 한다.
3. 가중치 규제(Regularization) 적용하기
복잡한 모델이 간단한 모델보다 과적합될 가능성이 높다. 그리고 간단한 모델은 적은 수의 매개변수를 가진 모델을 말한다. 복잡한 모델을 좀 더 간단하게 하는 방법으로 가중치 규제(Regularization)가 있다.
- L1 규제: 가중치들의 절대값 합계를 비용 함수에 추가한다. L1노름이라고도 한다. ➡️ 손실 함수에 가중치의 절대값을 더하는 방법
- L2 규제: 모든 가중치들의 제곱합을 비용 함수에 추가한다. L2노름이라고도 한다. ➡️ 손실함수 가중치의 제곱합을 더하는 방법
L1 규제 (손실 함수에 가중치의 절대값을 더한다)
손실 함수에 가중치의 절대값인 L1 노름(Norm)을 추가한다. 즉, 기존 비용 함수에 모든 가중치에 대해서 $$\lambda \mid w \mid$$를 더한 값을 비용 함수로 하는 것이다.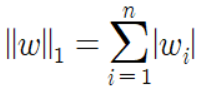
이를 여러 블로그에서 로지스틱 손실 함수에 적용해보는 경우가 많았다.
이때 규제의 양을 조절하는 $$\alpha$$를 적용하여 그냥 더하는 것이 아니라 $$\alpha$$를 곱한 후 더했다. 이후 이를 미분하여 이를 가중치 업데이트 식에 적용했다고 한다.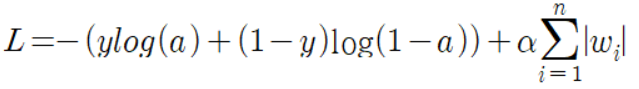
미분하면 $${ \partial \over \partial w} L = -(y-a)x +α × sign(w)$$ 꼴로 나오며 규제 하이퍼파라미터 $$\alpha$$와 가중치의 부호를 곱해서 업데이트할 그레디언트에 더해준다고 한다.
회귀 모델에 L1 규제를 추가한 것을 라쏘(Lasso)모델이라고 한다.
L2 규제
기존의 비용 함수에 모든 가중치에 대해서 $$\frac{1}{2} \lambda w^2$$를 더한 값을 비용함수로 한다. 이때 $$\lambda$$는 규제의 강도를 정하는 하이퍼파라미터이다.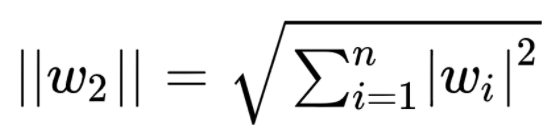
이것을 또한 로지스틱 손실함수에 적용하면 아래와 같은 식이 나온다고 한다.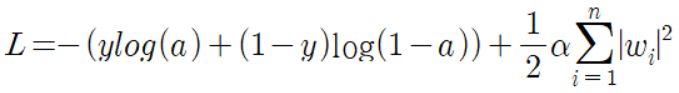
그리고 이 손실함수를 미분한 결과를 가중치 업데이트 식에 적용한다고 한다.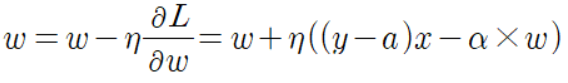
L1 vs L2
L1, L2 모두 비용함수를 최소화하기 위해서는 가중치 w들의 값ㅇ이 작아져야한다.
4. 드롭아웃(Dropout)
"신경망의 일부를 사용하지 않는 방법"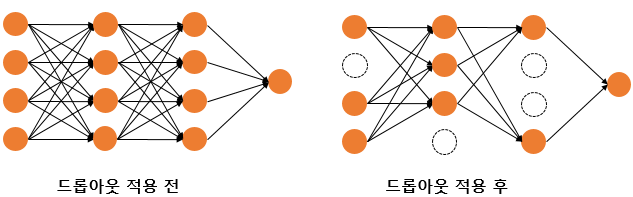
드롭아웃의 비율을 0.5로 한다면 학습 과정마다 랜덤의 절반 뉴런만을 사용한다.
드롭아웃은 신경망 학습 시에만 사용하고, 예측 시에는 사용하지 않는 것이 일반적이다. 학습 시에 특정 뉴런, 특정 조합에 너무 의존적이게 되는 것을 방지해주며, 매번 랜덤 선텍으로 뉴런을 사용하지 않기에 서로 다른 신경망들을 앙상블하여 사용하는 것 같은 효과를 내어 과적합을 방지한다. 케라스에서는 아래와 같은 방법으로 드롭아웃을 모델에 추가할 수 있다.
참고 사이트:
https://hyjykelly.tistory.com/51
https://rdmkyg.blogspot.com/2021/06/regularization-l1.html
'ML' 카테고리의 다른 글
| RAG/ LangChain 도입 (1) | 2024.07.14 |
|---|---|
| [만들면서 배우는 생성 AI]생성 모델링 (0) | 2024.06.05 |
| 역전파(BackPropagation) 이해하기 (1) | 2024.06.05 |
| 딥 러닝의 학습 방법 (1) | 2024.06.05 |
| 행렬곱으로 이해하는 신경망 (0) | 2024.06.05 |